Нахождение концентрации вещества при диффузии.
Найти распределение концентрации n(x,t)диффундирующего вещества в бесконечном слое0 <= x <= L,
-бесконечность < y, z < +бесконечность.
Поверхность х=0 непроницаема.
На поверхности x=L происходит массообмен с окружающей средой, имеющей концентрацию диффундирующего вещества:
dn/dx(L,t)=h*(A0*exp(-b*t)-n(L,t)) (задача №1.)
dn/dx(L,t)=A0*exp(-b*t) (задача №2.)
Начальная концентрация диффундирующего вещества внутри слоя постоянна и равна А0.
Коэффициент диффузии равен D (и равен h на границе x=L в задаче №1).
Составление дифференциального уравнения.
Рассмотрим бесконечно малый объём в виде прямого цилиндра с площадью основания S и образующей, направленной вдоль оси x , где длина образующей равна бесконечно малой величине dx .Координата левого конца равна x, координата правого конца равна x+dx.
В единицу времени через поверхность S, перепендикулярную оси x, пройдёт число молекул, пропорциональное градиенту концентрации вдоль оси x:
N=-D*dn/*dx*S
В единицу времени в объём цилиндра войдёт число молекул с левого конца, равное
Nвход = -D*S*dn/dx ,
где производная dn/dx берётся в точке x.
В единицу времени из объёма цилиндра выйдет число молекул с правого конца, равное
Nвыход= - D*S*dn/dx ,
где производная dn/dx берётся в точке x+dx
Для разности Nвход-Nвыход можно записать приближённое равенство:
Nвход-Nвыход= D*S*(d2n/dnx2)*dx
где d2n/dnx2 – вторая производная концентрации по координате x в точке x
(Точное равенство получится из теоремы Лагранжа, применяемой к первой производной, если вторую производную взять в некоторой точке интервала [x; x+dx] )
Разделив разность между числом входящих в цилиндр в единицу времени молекул и числом выходящих из цилиндра в единицу времени молекул на объём цилиндра S*dx, получим скорость изменения концентрации:
dn/dt=D*d2n/dx2
Получили уравнение диффузии: производная от концентрации n(x;t) по времени t равна произведению коэффициента диффузии на вторую производную от этой концентрации по координате x
Так как при x=0 поток равен нулю, то первая частная производная от концентрации n(x;t) по координате X равна нулю при x=0, то есть dn/dx(0,t)=0
Начальное условие: n(x,0)=A0 при t=0
Задача №1.


Задача №2.
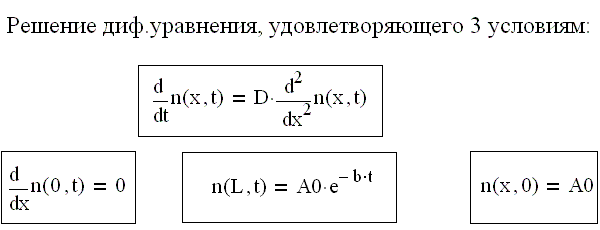

Программы.
Программа к задаче №1.Программа к задаче №2.
Программа строит графики зависимости n(x) и n(t)
в задаче №1 (ввести h ) и задаче №2 (при h=бесконечности)